Dilatometria
Dilatometria
Dilatação linear, superficial, volumétrica e dilatação dos líquidos
Dilatometria

Efeitos da dilatação sobre corpos sólidos

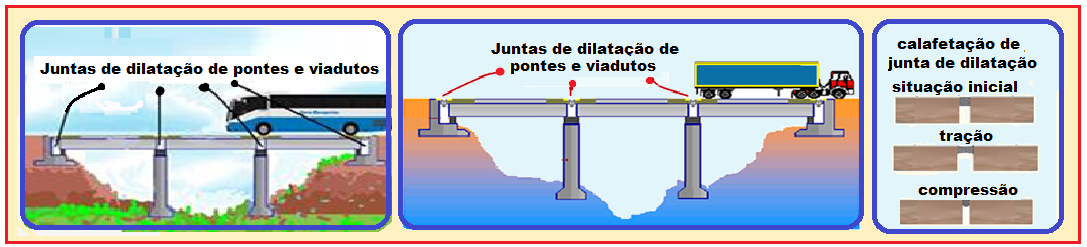

Dilatação linear dos sólidos
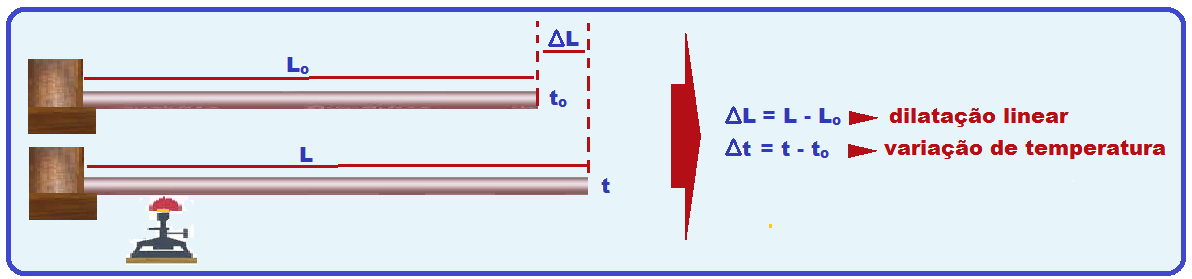
Trata-se da dilatação de uma das dimensões de um corpo, como por exemplo, seu comprimento. Considere uma haste metálica de comprimento Lo e à temperatura to.
Quando aquecida terá comprimento L a uma temperatura t.
Características da dilatação linear
A dilatação linear ΔL é diretamente proporcional à variação de temperatura Δt.
A dilatação linear ΔL é diretamente proporcional ao comprimento inicial Lo.
A dilatação linear ΔL depende do material de que é constituído o corpo.
Matematicamente:

Sendo:
ΔL ![]() dilatação linear (de quanto dilatou o comprimento ou uma dimensão)
dilatação linear (de quanto dilatou o comprimento ou uma dimensão)
α ![]() coeficiente de dilatação linear médio, característica do material que constitui a barra.
coeficiente de dilatação linear médio, característica do material que constitui a barra.
Lo ![]() comprimento inicial
comprimento inicial
L ![]() comprimento final
comprimento final
Δt ![]() intervalo de temperatura
intervalo de temperatura
Unidades do coeficiente de dilatação linear α
Isolando α na equação ΔL = Lo.α.Δt ![]() α =
α = 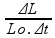
![]() como Lo e ΔL devem ter a mesma unidade, elas se cancelam
como Lo e ΔL devem ter a mesma unidade, elas se cancelam ![]() então a unidade em que se exprime o coeficiente de dilatação linear é o
então a unidade em que se exprime o coeficiente de dilatação linear é o
![]()
Observe que o coeficiente de dilatação linear representa a dilatação de um corpo de comprimento unitário, quando sua temperatura varia de um grau.
Gráfico do comprimento L em função da temperatura θ

Aplicações práticas de dilatação linear
![]()
Lâminas bimetálicas
Quando você solda duas barras de materiais diferentes você obtém uma lâmina bimetálica e, se você as submeter à mesma variação de temperatura, o sistema vai curvar-se para o lado da barra de menor coeficiente de dilatação, quando aquecida e para o lado da barra de maior coeficiente de dilatação, quando resfriada.
Observe nas figuras abaixo uma lâmina bimetálica constituída de alumínio (αaluminio=22.10-6 oC-1) e invar (liga de ferro e níquel – αinvar=1,0 .10-6 oC–1) e observe como a lâmina se inclina quando a temperatura aumenta ou diminui.

As lâminas bimetálicas são muito utilizadas nos relés térmicos (termostatos – dispositivos que
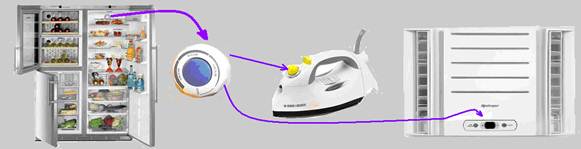
desligam automaticamente um circuito quando a temperatura atinge determinado valor) para controlar a temperatura de um dado ambiente, nas geladeiras, freezers, ferro elétrico automático, aparelhos de ar condicionado, fornos de fogões elétricos, etc.
Quando a temperatura do ambiente superar certo limite, o termostato deve desligar o aquecedor fazendo sua lâmina bimetálica envergar, abrindo os contatos, e desligando o aparelho da rede elétrica.
Quando a temperatura cair abaixo de certo limite, o aquecedor deve ser novamente ligado com a lâmpada curvando-se em sentido oposto e fecha os contatos.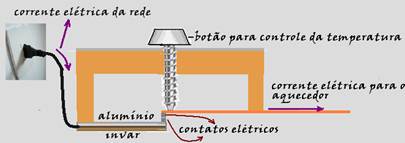
Esse mesmo processo é utilizado na prevenção de incêndio por motivo de sobrecarga elétrica, desligando o circuito quando a temperatura atingir certos limites.
![]()
Nos ferros elétricos automáticos, a temperatura de funcionamento, que é previamente regulada por um parafuso, é controlada por um termostato constituído de duas lâminas bimetálicas de igual composição.
Os dois metais que formam cada uma das lâminas têm coeficientes de dilatação αI (o mais interno) e αII o mais externo). As duas lâminas estão encurvadas e dispostas em contato elétrico, uma no interior da outra, como indicam as figuras.
A corrente, suposta contínua, entra pelo ponto 1 e sai pelo ponto 2, conforme a figura 1, aquecendo a resistência. 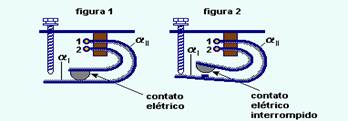
À medida que a temperatura aumenta, as lâminas vão se encurvando, devido à dilatação dos metais, sem interromper o contato.
Quando a temperatura desejada é alcançada, uma das lâminas é detida pelo parafuso, enquanto a outra continua encurvando-se, interrompendo o contato entre elas, conforme a figura 2.
Observe que as lâminas estão se encurvando para dentro, então α2 > α1 e, quanto mais baixo estiver o contato (mais apertado o parafuso), menor será a dilatação das lâminas e consequentemente menor será a temperatura.
![]()
Lâmpada Pisca-pisca
Quando você liga a lâmpada, a corrente elétrica flui da lâmina bimetálica para o filamento no qual

ela está em contato, que, por sua vez flui para todos os outros, tornando-os incandescentes e acendendo a lâmpada.
Quando a lâmina bimetálica ficar suficientemente quente ela se encurvará, interrompendo a corrente elétrica e apagando a lâmpada.
Em seguida ela se resfria e se curva, restabelecendo o contato e acendendo novamente a lâmpada.
E assim por diante.
![]()
Termômetro de lâmina bimetálica

Constituído por duas lâminas bimetálicas com metais diferentes, e soldadas uma com a outra, conforme a figura.
Sendo os metais diferentes, quando aquecidos eles sofrem diferentes dilatações, provocando um encurvamento diferente da lâmina para cada variação de temperatura.
São muito usados no controle de temperaturas de fornos, saunas, etc.
Dilatação superficial dos sólidos
Um corpo sólido sofre dilatação superficial quando sofre aumento em duas de suas dimensões.
Considere uma placa metálica de comprimento Co, largura Lo e espessura desprezível, que se encontra a uma temperatura to.
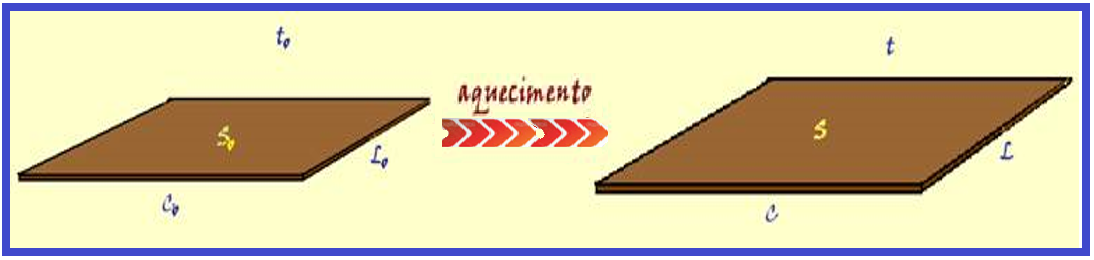
A área de sua superfície antes do aquecimento será So = Co.Lo e após o aquecimento será S = C.L.
Todas as leis válidas para a dilatação linear são também válidas para a dilatação superficial, ou seja:
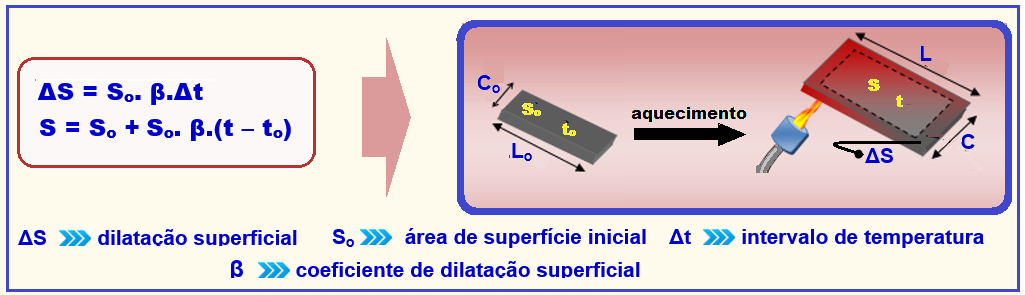
Na expressão acima, a letra grega β (beta) é uma grandeza constante, característica do material, denominada coeficiente de dilatação superficial médio.
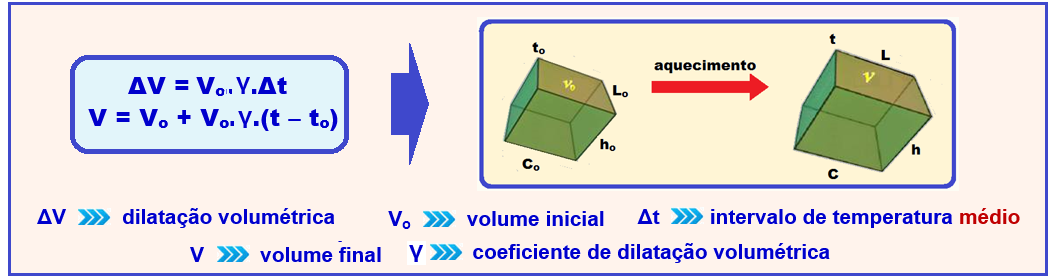
Dilatação volumétrica ou cúbica dos sólidos
A dilatação volumétrica ou cúbica ocorre quando, devido a uma elevação de temperatura, um corpo
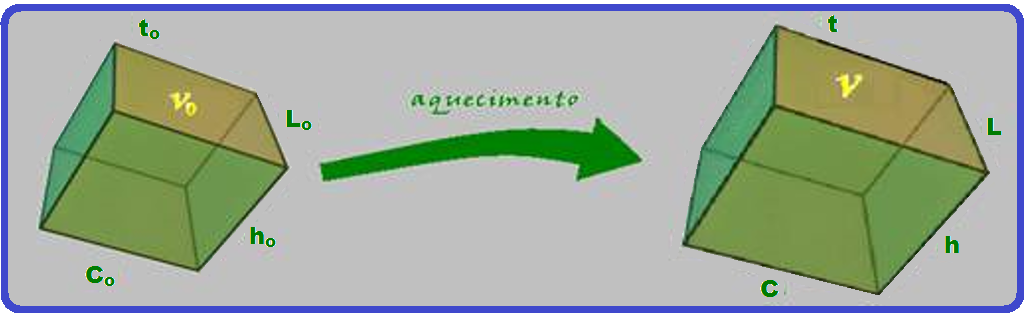
sofre um aumento em suas três dimensões (volume).
Todas as leis válidas para as dilatações linear e superficial são também válidas para a dilatação volumétrica, ou seja:
Relação entre os coeficientes de dilatação linear, superficial e volumétrica.

Dilatação dos líquidos
Os líquidos são amorfos, ou seja, não possuem forma própria, adquirindo o formato do recipiente

onde estão contidos.
Por esse motivo sofrem apenas dilatação volumétrica.
Dilatação aparente dos líquidos
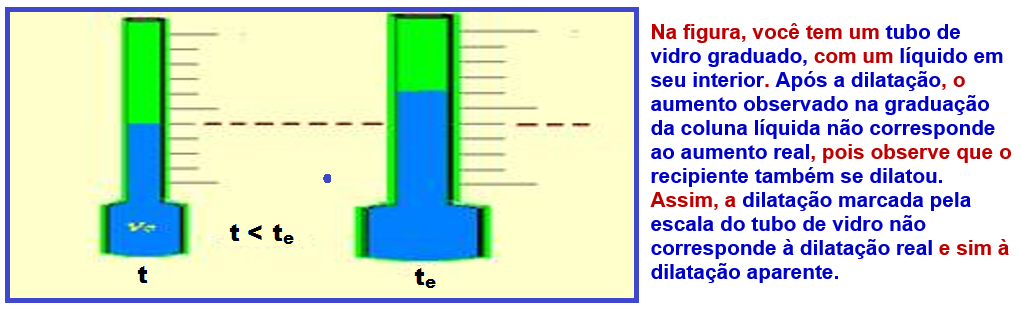
Dilatação real ou absoluta
Nela, leva-se em conta apenas a dilatação do líquido, sem considerar a dilatação do recipiente.
Pode-se verificar que um mesmo líquido, em diferentes frascos, possui um só coeficiente de dilatação absoluta ou real, característico desse líquido.
Porém, tem vários coeficientes de dilatação aparente, dependendo da natureza dos frascos que a encerram.
Dilatação do frasco
Lembre-se de que o frasco se comporta como se fosse maciço e constituído do mesmo material das paredes do recipiente.
Assim, o coeficiente de dilatação que se deve usar é o coeficiente de dilação do material de que é feito o frasco.
Equações que envolvem a dilatação dos líquidos
Observe atentamente as explicações a seguir:
O frasco da figura abaixo contém um “ladrão” com o líquido preenchendo o recipiente até seu nível (figura I).
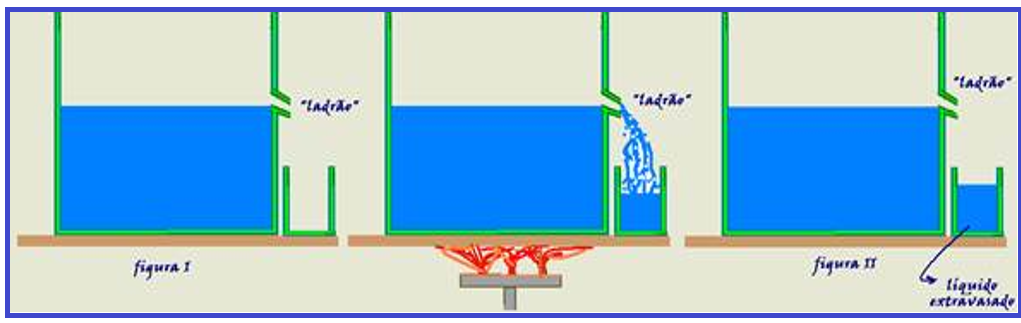
Após o conjunto ser aquecido de Δt, como normalmente os líquidos se dilatam mais que os sólidos, parte do líquido extravasa pelo “ladrão” (figura II).
Esse volume de líquido extravasado corresponde à dilatação aparente do líquido (ΔVap), de volume inicial Vo e coeficiente de dilatação volumétrica aparente (γap) e não à dilatação real do líquido, já que o frasco também se dilata.
Se você conhecer a dilatação do frasco (ΔVf) que corresponde à quanto seu volume aumentou, poderá determinar a dilatação real sofrida pelo líquido.
Exemplo numérico:
Se o volume do frasco que contém o líquido (até o nível do “ladrão), aumentar, por exemplo, de 1 cm3 (ΔVf) = 1 cm3 e, se o volume de líquido extravasado for de 3 cm3 (ΔVap = 3 cm3), você pode obter a dilatação real do líquido (ΔVR), pois, ΔVR = ΔVap + ΔVf ![]() ΔVR = 3 + 1 = 4 cm3.
ΔVR = 3 + 1 = 4 cm3.
Equações:
![]() Dilatação real do líquido
Dilatação real do líquido ![]() ΔVR = Vo.γlíquido.Δt
ΔVR = Vo.γlíquido.Δt ![]() (Vo
(Vo ![]() volume inicial do líquido)
volume inicial do líquido)
 Dilatação aparente (volume de líquido extravasado)
Dilatação aparente (volume de líquido extravasado) ![]() ΔVap = Vo.γap.Δt
ΔVap = Vo.γap.Δt ![]() (Vo
(Vo ![]() volume inicial do líquido)
volume inicial do líquido)
![]() Dilatação do frasco (recipiente)
Dilatação do frasco (recipiente) ![]() ΔVf = Vo.γfrasco.Δt
ΔVf = Vo.γfrasco.Δt ![]() (Vo
(Vo ![]() volume inicial do líquido)
volume inicial do líquido)
![]() ΔVR = ΔVap + ΔVf (veja exemplo numérico acima)
ΔVR = ΔVap + ΔVf (veja exemplo numérico acima)
![]() γR = γap + γfrasco ( R é o coeficiente de dilatação volumétrica real do líquido ap é o coeficiente de dilatação volumétrica aparente e frasco é o coeficiente de dilatação volumétrica do frasco).
γR = γap + γfrasco ( R é o coeficiente de dilatação volumétrica real do líquido ap é o coeficiente de dilatação volumétrica aparente e frasco é o coeficiente de dilatação volumétrica do frasco).
Analise alguns exercícios resolvidos sobre dilatação dos líquidos


Um frasco de capacidade para 10 litros está completamente cheio de glicerina e encontra-se à temperatura de 10ºC.
Aquecendo-se o frasco com a glicerina até atingir 90ºC, observa-se que 352 mL de glicerina transborda do frasco.
Sabendo-se que o coeficiente de dilatação volumétrica da glicerina é
5,0.10-4 ºC-1, calcule o coeficiente de dilatação linear do frasco é ºC-1.
São dados: Vo = 10 L (do frasco e da glicerina) ![]() to = 10 oC
to = 10 oC ![]() t = 90 oC
t = 90 oC ![]() ΔVap = 352 mL = 352.
ΔVap = 352 mL = 352.
10-3 L ![]() γglicerina = 5,0.10-4 oC-1.
γglicerina = 5,0.10-4 oC-1.
O volume de glicerina que extravasou corresponde à dilatação aparente ![]() ΔVap = Vo. γap.Δt
ΔVap = Vo. γap.Δt ![]()
352.10-3 = 10.γap.(90 – 10) ![]() γap =
γap =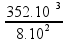
![]() γap = 44.10-5 oC-1.
γap = 44.10-5 oC-1.
γglicerina = γap+ γf ![]() 5,0.10-4 = 44.10-5 + γf
5,0.10-4 = 44.10-5 + γf ![]() γf = 5,0.10-4 – 4,4.10-4
γf = 5,0.10-4 – 4,4.10-4 ![]() γf = 6,0.10-5 oC-1 (coeficiente de dilatação volumétrica do frasco).
γf = 6,0.10-5 oC-1 (coeficiente de dilatação volumétrica do frasco).
Acontece que o exercício quer o coeficiente de dilatação linear do frasco αf = γf/3
αf = 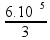
![]() αf = 2,0.10-5 oC-1 .
αf = 2,0.10-5 oC-1 .


A dilatação aparente corresponde ao aumento na indicação da escala ![]() ΔVap = 525 – 500 = 25 cm3
ΔVap = 525 – 500 = 25 cm3 ![]() ΔVap = Vo.γap.Δt
ΔVap = Vo.γap.Δt ![]() 25 = 500.γap.50
25 = 500.γap.50 ![]() γ p=
γ p= 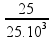
![]() γap = 10-3 oC-1.
γap = 10-3 oC-1.
γlíq = γV + γap ![]() γlíq = 0,001 + 0,00001
γlíq = 0,001 + 0,00001 ![]() γlíq = 0,00101 oC-1.
γlíq = 0,00101 oC-1.
![]()
Um recipiente de vidro tem capacidade de 100cm3 a 10oC e contém, a essa temperatura, 99cm3 de um certo líquido de coeficiente de dilatação cúbica γ = 2.10-4 oC-1. A que temperatura o recipiente estará completamente cheio de líquido?
(Considere o coeficiente de dilatação cúbica do vidro como sendo
10-5 oC-1).
Quando o recipiente estiver completamente cheio de líquido, eles (recipiente e líquido) deverão ter o mesmo volume ![]() ΔVvidro = ΔVlíquido
ΔVvidro = ΔVlíquido ![]() 100(1 + 10-5 (t – 10) = 99.(1 + 2.10-4).(t – 10)
100(1 + 10-5 (t – 10) = 99.(1 + 2.10-4).(t – 10) ![]()
t = 19,6.10-2 /18,6.10-3 ![]() t ≈ 10,5 oC.
t ≈ 10,5 oC.
![]()
Um recipiente de vidro encontra-se completamente cheio de um líquido a 0 ºC. Quando o
conjunto é aquecido até 80 ºC, o volume do líquido que transborda corresponde a 4% do volume
que o líquido possuía a 0 ºC. Sabendo que o coeficiente de dilatação volumétrica do vidro é igual
a 27.10-6 ºC-1, determine o coeficiente de dilatação real do líquido.
Vo = volume inicial do recipiente = volume inicial do líquido a 0oC.
Dilatação do vidro com Vo = volume inicial do líquido ![]() V = Vo.(1+γ.(t – to)
V = Vo.(1+γ.(t – to) ![]() V = Vo.(1+.27.10-5 .80)
V = Vo.(1+.27.10-5 .80) ![]() V = 1,00216.Vo (volume final do recipiente).
V = 1,00216.Vo (volume final do recipiente).
O líquido se dilatou V’ que é o volume do recipiente V + o volume de líquido derramado que é de 4% de Vo.
V’ = V + 0,04Vo ![]() Dilatação do líquido
Dilatação do líquido ![]() V’ = Vo.(1+γ’.Δt) onde γ’ é o coeficiente de dilatação aparente do líquido.
V’ = Vo.(1+γ’.Δt) onde γ’ é o coeficiente de dilatação aparente do líquido.
V’ = V + 0,04Vo ![]() V’ = (1,00216Vo) + 0,04Vo
V’ = (1,00216Vo) + 0,04Vo ![]() V’ = 1,04216Vo
V’ = 1,04216Vo
V’ = Vo.(1+γ’.Δt) ![]() 1,04216Vo = Vo(1+γ’.80)
1,04216Vo = Vo(1+γ’.80) ![]() 1,04216 = 1 + 80γ’
1,04216 = 1 + 80γ’ ![]()
80γ’=0,04216 ![]() γ’ = 5,27.10-4 ºC-1.
γ’ = 5,27.10-4 ºC-1.
O que você deve saber, orientações e dicas
![]()

Sendo:
ΔL ![]() dilatação linear (de quanto dilatou o comprimento ou uma dimensão)
dilatação linear (de quanto dilatou o comprimento ou uma dimensão)
α ![]() coeficiente de dilatação linear médio, característica do material que constitui a barra.
coeficiente de dilatação linear médio, característica do material que constitui a barra.
Lo ![]() comprimento inicial
comprimento inicial
L ![]() comprimento final
comprimento final
Δt ![]() intervalo de temperatura
intervalo de temperatura
![]()

![]()
Se as armações metálicas das figuras forem de mesmo material, homogêneas e de secção transversal constante e se sofrerem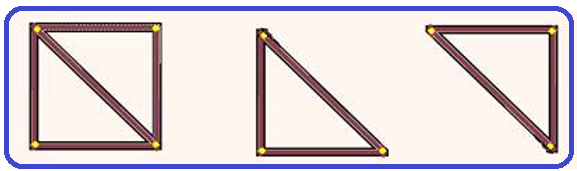
a mesma variação de temperatura (por exemplo, sendo aquecidas), elas não se deformarão, os pontos de contato não trocarão forças entre si, elas manterão o formato inicial, mas com dimensões maiores e, todos os ângulos internos permanecerão os mesmos.
Observe que seus comprimentos não se dilatam por igual, a hipotenusa se dilata mais que os catetos.
![]()
Lâminas bimetálicas
Quando você solda duas barras de materiais diferentes você obtém uma lâmina bimetálica e, se você as submeter à mesma variação de temperatura, o sistema vai curvar-se para o lado da barra de menor coeficiente de dilatação, quando aquecida e para o lado da barra de maior coeficiente de dilatação, quando resfriada.
Observe nas figuras abaixo uma lâmina bimetálica constituída de alumínio (αaluminio = 22.10-6 oC-1) e

invar (liga de ferro e níquel, αinvar = 1,0 .10-6 oC-1) e observe como a lâmina se inclina quando a temperatura aumenta ou diminui.
![]()
Utilidades das lâminas bimetálicas
As lâminas bimetálicas são muito utilizadas nos relés térmicos (termostatos, que são dispositivos que desligam automaticamente um circuito quando a temperatura atinge determinado valor) para controlar a temperatura de um dado ambiente, nas geladeiras, freezers, ferro elétrico automático, aparelhos de ar condicionado, fornos de fogões elétricos, etc.
Quando a temperatura do ambiente superar certo limite, o termostato deve desligar o aquecedor fazendo sua lâmina bimetálica envergar abrindo os contatos, e desligando o aparelho da rede elétrica.
Quando a temperatura cair abaixo de certo limite, o aquecedor deve ser novamente ligado com a lâmpada curvando-se em sentido oposto e fecha os contatos.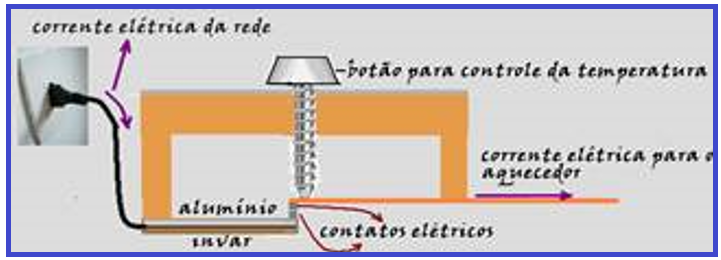
Esse mesmo processo é utilizado na prevenção de incêndio por motivo de sobrecarga elétrica, desligando o circuito quando a temperatura atingir certos limites.
![]()

![]()

![]()
Pêndulo simples
Trata-se de corpo de massa m suspenso por um fio inextensível e de massa desprezível.
Quando afastado de sua posição de equilíbrio e solto, o pêndulo oscilará em um plano vertical sob à ação da gravidade g; o movimento é periódico e oscilatório e o seu período (tempo que ele demora para efetuar um “vai e vem” completo) é fornecido por T=2π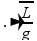
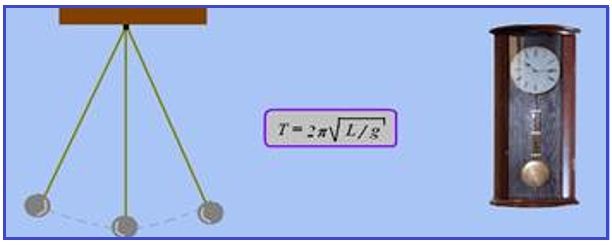
O Pêndulo Simples, através da equação acima, também fornece um método para medições do valor da aceleração da gravidade g num dado local, medindo-se o comprimento do fio L e o período de oscilação T, substituindo esses dois dados na equação acima você acha o valor da aceleração da gravidade g nesse local.
Observe que o período T, é independente da massa m do corpo suspenso (não aparece na fórmula).
![]()
![]()
Veja a resolução desse exercício:
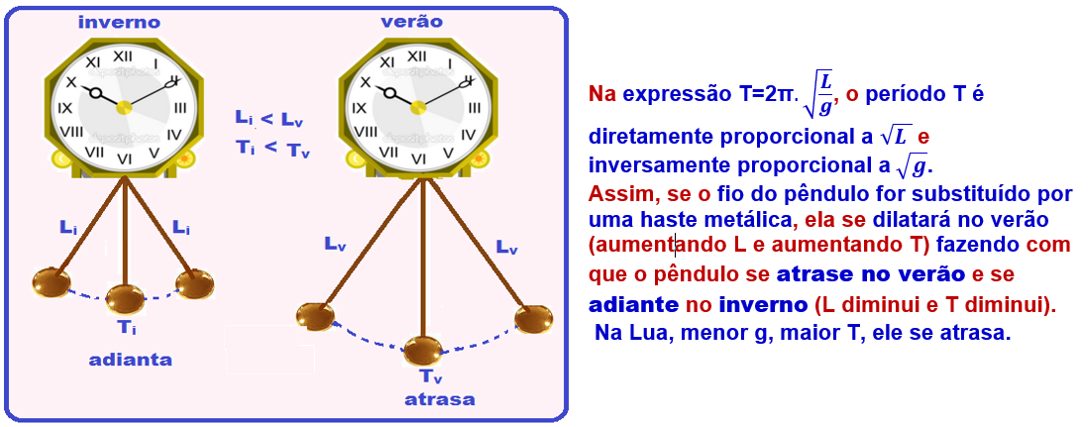
A figura mostra uma ponte apoiada sobre dois pilares feitos de materiais diferentes.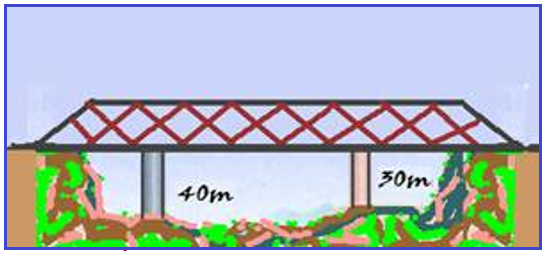
Como se vê, o pilar mais longo, de comprimento L1 = 40 m, possui coeficiente de dilatação linear α = 18. 10-6 °C-1.
O pilar mais curto tem comprimento L2 = 30 m. Para que a ponte permaneça sempre na horizontal, determine o coeficiente linear do material do segundo pilar.
Para que a ponte permaneça sempre na horizontal, os dois pilares devem sofrer a mesma dilatação para a mesma variação de temperatura ![]() ΔL1= ΔL2
ΔL1= ΔL2 ![]() L01.α1.Δt = L02.α2.Δt
L01.α1.Δt = L02.α2.Δt ![]() 40.18.10-6 = 30.α2
40.18.10-6 = 30.α2 ![]() α2 = 24.10-6 oC-1.
α2 = 24.10-6 oC-1.
![]()

![]()
Se uma placa metálica com orifício for aquecida, verifica-se que o orifício aumenta, como se fosse

constituído pelo material da placa, pois tudo se passa como se o furo tivesse um coeficiente de dilatação superficial igual àquele da substância da placa.
![]()
Se você despejar água fervente num copo de vidro, ele pode se quebrar, pois a dilatação não é uniforme, a parte interna se dilata mais que a externa.
O mesmo poderia ocorrer se você despejasse água gelada num copo quente e, nesse caso a parte interna se contrai mais que a externa.
Se você despejar água fervente num copo de vidro até a metade, ele pode quebrar mais facilmente do que quando cheio completamente, porque a temperatura dele muda uniformemente, o que causa a quebra do copo é o fato de que a parte de baixo fique mais quente e se dilate mais do que a de cima, podendo provocar a ruptura.
![]()
Observe também que se você tiver dois copos de diferentes coeficientes de dilatação, o de menor coeficiente apresenta maior
dificuldade de se quebrar quando aquecido, pois se dilata menos.
![]()

![]()

![]()
Se as duas esferas da figura abaixo forem idênticas (mesmas dimensões e mesmo material) e sofrerem a mesma variação de temperatura, elas sofrem a mesma dilatação volumétrica. 
Corpos ocos se dilatam como se fossem maciços e sua dilatação é calculada utilizando o coeficiente de dilatação volumétrica do material que constitui sua superfície.
O mesmo acontece se ele tiver um furo, e se a esfera com o furo for aquecida, verifica-se que o furo aumenta, como se fosse como se fosse constituído pelo material da esfera.
Assim, o furo se comporta como tivesse o mesmo coeficiente de dilatação volumétrica que o da substância que constitui a esfera.
![]()
Equações utilizadas na dilatação de líquidos
![]() Dilatação real do líquido
Dilatação real do líquido ![]() ΔVR = Vo.γlíquido.Δt
ΔVR = Vo.γlíquido.Δt ![]() (Vo
(Vo ![]() volume inicial do líquido)
volume inicial do líquido)
![]() Dilatação aparente (volume de líquido extravasado)
Dilatação aparente (volume de líquido extravasado) ![]() ΔVap = Vo.γap.Δt
ΔVap = Vo.γap.Δt ![]() (Vo
(Vo ![]() volume inicial do líquido)
volume inicial do líquido)
![]() Dilatação do frasco (recipiente)
Dilatação do frasco (recipiente) ![]() ΔVf = Vo.γfrasco.Δt
ΔVf = Vo.γfrasco.Δt ![]() (Vo
(Vo ![]() volume inicial do líquido)
volume inicial do líquido)
![]() ΔVR = ΔVap + ΔVf (veja exemplo numérico acima)
ΔVR = ΔVap + ΔVf (veja exemplo numérico acima)
![]() γR = γap + γfrasco ( R é o coeficiente de dilatação volumétrica real do líquido ap é o coeficiente de dilatação volumétrica aparente e frasco é o coeficiente de dilatação volumétrica do frasco).
γR = γap + γfrasco ( R é o coeficiente de dilatação volumétrica real do líquido ap é o coeficiente de dilatação volumétrica aparente e frasco é o coeficiente de dilatação volumétrica do frasco).
![]()
O coeficiente de dilatação aparente depende da natureza do líquido e do material que constitui o recipiente que o contém.
