Associação de espelhos planos Resoluções

 

01- n=360/α – 1  ---  n=360/24 – 1  --- n=15 – 1  ---  n=14 imagens  ---  no plano bissetor do ângulo formado entre os dois espelhos.

02- n=360/β – 1  ---  8=360/β – 1  ---  360/β=9  ---  β=40o 

03- R- A (veja teoria)

04- R – A  (veja teoria)

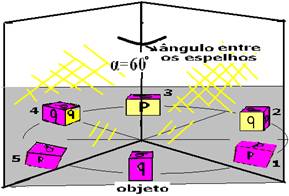
05- A expressão n=360/α – 1 só é válida para um objeto  ---  n=360/60 – 1  ---  n=5 imagens  ---  2 indivíduos – 10 imagens + os  2 objetos  ---   na foto aparecem 12 indivíduos.

06- A imagem frontal aos dois espelhos está de frente para o objeto e objeto e imagem frontal não são reversos ou revertidos, ou seja, não trocam direita pela esquerda.

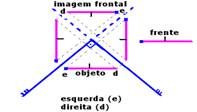
R- A

07- Observe que o ângulo entre os dois espelhos planos é α=360 – 120=240^o e que o ponto A está no plano bissetor ---   n=360/α – 1  ---  n=360/240 – 1=1,5 – 1=0,5, ou seja, nenhuma imagem 

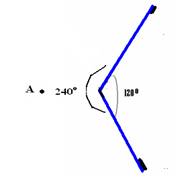
ou ainda, observe nas figuras abaixo que o observador que está no ponto A está fora de seu campo visual no espelho E’ (figura 1)

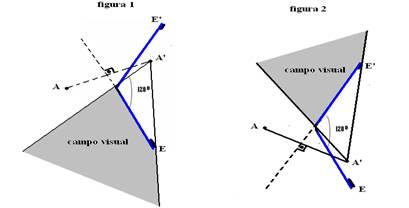
 e E (figura 2).

08- b) α=5n  ---  n=360/α – 1  ---  n=360/5n – 1  ---  n + 1=360/5n  ---  n² + n -72=0  ---  n=(-1 + 17)/2  ---  n= 8 imagens

a) α=5.8  ---  α=40^o

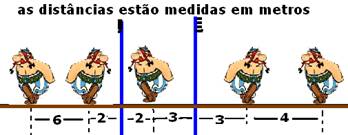
09- São 72 soldados no filme menos 6 soldados objetos=66 soldados imagens de 6soldados objetos  ---   regra de três  ---  6 objetos – 66 imagens – 1 objeto – n=66/6=11 imagens  ---  n=360/α – 1  ---  11=360/α – 1  ---  α=360/12  ---  α=30^o

10- Observe as figuras abaixo onde a primeira imagem P’ (conjugada pelo espelho E) funciona como objeto para o espelho E’,

 

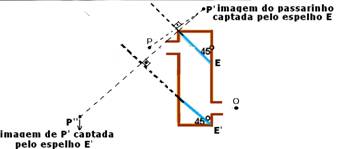
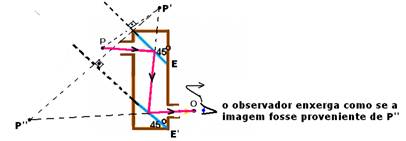
originando a imagem P’’, que é vista pelo observador (figura da esquerda) e os raios de luz que possibilitam essa visualização estão na figura da direita. Esses dois espelhos planos que constituem o periscópio fornecem, a partir da luz proveniente de um objeto real (no caso, o passarinho), uma imagem final P’’ virtual, do mesmo tamanho do objeto e não reversa (não troca direita pela esquerda).

11- a), b) e c)

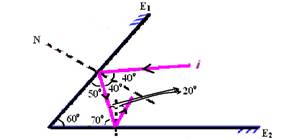
12-- R- D  (observe a figura abaixo)

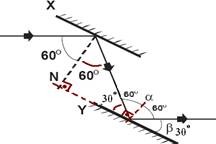
13- R – B  (veja figura abaixo)

14- Como a imagem da foto do quadro é invertida e reversa, o quadro original Q, que é o objeto, e que terá a seguinte aparência . O sistema de espelhos deixa a imagem desse objeto, invertendo-o e revertendo-o  conforme a figura a seguir .

A máquina fotográfica capta a imagem anterior, invertendo-a e revertendo-a novamente e deixando-a como na figura a. R- A

15- Na figura abaixo todas as faces do cubo tem o símbolo e a face que está voltada para o espelho tem cor amarela.

Observe que, das 5 imagens formadas, apenas nas 2, 3 e 4 aparecem a face voltada para o espelho e apenas nas 2 e 4 o símbolo está escrito corretamente, que no exercício corresponde às imagens 3 e 5.

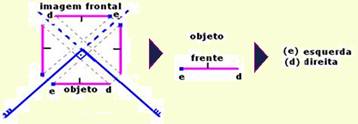
16- Observe que o sistema A corresponde a um periscópio onde a imagem do objeto é idêntica ao mesmo e de mesmas dimensões. O sistema B não é um periscópio, formando uma imagem invertida (troca cima por baixo) e reversa ou revertida (troca direita pela esquerda) - R- B

17- Regra de três  ---  π rad – 180^o  ---  π/3 rad – α  ---  180.π/3=πα  ---  α=60^o  ---  n=360/60 – 1  ---  n= 5 imagens  R- C

18- R- E  (veja teoria)

19- tan5,7=cateto oposto/cateto adjacente  ---  0,1=x/1,00  ---  x=0,1m  ---  observe na figura abaixo que para cada reflexão temos

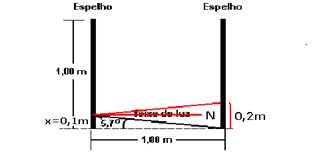
0,2m. Assim, 1,00/0,2=5 reflexões  R- B

20-

R- B

21- R- A  (veja teoria)

22- A imagem frontal aos dois espelhos está de frente para o objeto e objeto e imagem frontal não são reversos ou revertidos, ou seja, não trocam direita pela esquerda mas são direitos e não invertidos. Assim, se o objeto for FÍSICA, a imagem frontal também será FÍSICA. R- C.

23- R- JÁ  Periscópios fornecem sempre imagens direitas, virtuais, não revertidas e de mesmas dimensões que o objeto.

24- R- D  (veja resposta 16 – sistema B)

25- Para que os raios de luz retornem pela mesma trajetória que incidiram, eles devem incidir no espelho horizontal com ângulo

de 90^o e, pela figura abaixo observa-se que a alternativa correta é a C.

 

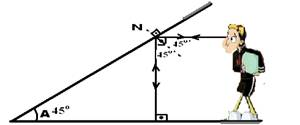
26- Observe que  α = 4 n  ---  o número de imagens (n) obtidas pela associação de dois espelhos planos que formam entre si um ângulo α (em graus) é dado pela expressão  ---  n=(360/ α) – 1  ---  n=(360/4n) – 1  ---  n² + n -90=0  ---  n=-1 ± √(1² + 360)/2  --- 

n= (- 1 ± 19)/2  ---  desprezando a resposta negativa  ---  n=9  ---  α=4n  ---  α=36^o

 

27-(PUC-SP-012)

A expressão que fornece o número de imagens n em função do ângulo θ entre os espelhos é  ---  n=360/θ – 1 ( I )  ---  para o ângulo θ/4 o número de imagens será m tal que  ---  m=360/(θ/4) – 1  ---  m=1440/θ – 1 ( II )  ---  isolando θ em ( I )  --- 

n + 1 = 360/θ  ---  θ=360/(n + 1)  ---  isolando θ em ( II )  ---  m +  1=1440/θ  ---  θ=1440/(m + 1)  ---  igualando-as  --- m

360/(n + 1)= 1440/(m + 1)  ---  4(n + 1)=m + 1  ---  4n + 4=m + 1  ---  m=4n + 3  ---  R- A

 28-(UNESP-SP-012)

 O enunciado pede para admitir que os ângulos de incidência e de reflexão do feixe de luz sobre um espelho sejam iguais  ---  isso significa que os ângulos de incidência e de reflexão do raio de luz são iguais sendo que o mesmo deve acontecer com os ângulos alternos internos (veja figura)  ---  observe que, se você dividir a distância h nas 4 partes indicadas, você terá que h=h₁ + h₂ + h₃ +

 

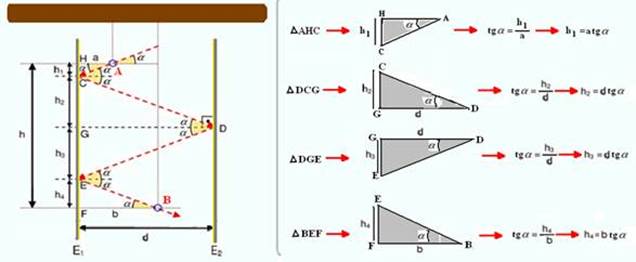
h₄  ---  h= atgα + dtgα + dtgα + btgα  ---  h=tgα(a + 2d + b)  ---  tgα=h/(a + 2d + b)  ---  α=arctg[h/(a + 2d + b)].