Exercícios de vestibulares com resolução comentada sobre Energia Mecânica
Exercícios de vestibulares com resolução comentada sobre
Energia Mecânica
01-(UFMG-MG) Rita está esquiando numa montanha dos Andes. A energia cinética dela em função do tempo, durante parte do trajeto, está representada neste gráfico:

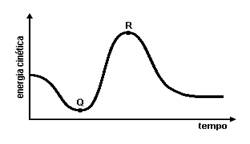
Os pontos Q e R, indicados nesse gráfico, correspondem a dois instantes diferentes do movimento de Rita.
Despreze todas as formas de atrito.
Com base nessas informações, é CORRETO afirmar que Rita atinge
a) velocidade máxima em Q e altura mínima em R.
b) velocidade máxima em R e altura máxima em Q.
c) velocidade máxima em Q e altura máxima em R.
d) velocidade máxima em R e altura mínima em Q.
02-(Ufsm-RS) A figura a seguir, representa uma barragem com a canalização que leva a água à turbina.
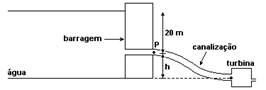
Se não existe perda de energia no escoamento e se o módulo da velocidade da água em P é v, a energia disponível para girar a turbina, para uma quantidade de água de massa m, é:
a) (1/2) mv2 + mgh
b) mgh
c) (1/2) mv2 – mgh
d) (1/2) mv2
e) (1/2) mv2 + mg(20m + h)
03-(PUC-RJ) Determine a massa de um avião viajando a 720km/h, a uma altura de 3.000 m do solo, cuja energia mecânica total é de 70,0.106 J
Considere a energia potencial gravitacional como zero no solo.(g=10m/s2)
![]()
04-(PUC-RJ) Uma pedra, deixada cair de um edifício, leva 4s para atingir o solo.
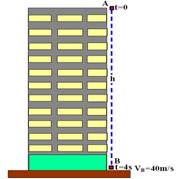
Desprezando a resistência do ar e considerando g = 10 m/s2, escolha a opção que indica a altura do edifício em metros.
![]()
05-(PUC-MG) Um ciclista desce uma rua inclinada, com forte vento contrário ao seu movimento, com velocidade constante.

Pode-se afirmar que:
a) sua energia cinética está aumentando.
b) sua energia potencial gravitacional está diminuindo
c) sua energia cinética está diminuindo.
d) sua energia potencial gravitacional é constante.
06-(PUC-MG) Os gatos conseguem sair ilesos de muitas quedas. Suponha que a maior velocidade que ele possa atingir o solo, sem se machucar, seja de 29 km/h. Então, desprezando-se a resistência do ar e considerando g = 10m/s2, a altura máxima de queda para que um gato, partindo do repouso, nada sofra é, aproximadamente, de:
![]()
07- (Uffrj-RJ) O salto com vara é, sem dúvida, uma das disciplinas mais exigentes do atletismo. Em um único salto, o atleta executa cerca de 23 movimentos em menos de 2 segundos. Na última Olimpíada de Atenas a atleta russa, Svetlana Feofanova, bateu o recorde feminino, saltando 4,88 m.
A figura a seguir representa um atleta durante um salto com vara, em três instantes distintos.

Assinale a opção que melhor identifica os tipos de energia envolvidos em cada uma das situações I, II, e III, respectivamente.
a) – cinética – cinética e gravitacional – cinética e gravitacional
b) – cinética e elástica – cinética, gravitacional e elástica – cinética e gravitacional
c) – cinética – cinética, gravitacional e elástica – cinética e gravitacional
d) – cinética e elástica – cinética e elástica – gravitacional
e) – cinética e elástica – cinética e gravitacional – gravitacional
08-(Ufpe) Com base na figura a seguir, calcule a menor velocidade com que o corpo deve passar pelo ponto A para ser capaz de atingir o ponto B. Despreze o atrito e considere g = 10 m/s2.

09-(PUC-RS) Um bloco de 4,0 kg de massa, e velocidade de 10m/s, movendo-se sobre um plano horizontal, choca-se contra uma mola, como mostra a figura
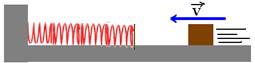
Sendo a constante elástica da mola igual a 10000N/m, o valor da deformação máxima que a mola poderia atingir, em cm, é
![]()
10-(UNICAMP-SP) Um brinquedo que muito agrada às crianças são os lançadores de objetos em uma pista. Considere que a mola da figura a seguir possui uma constante elástica k = 8000 N/m e massa desprezível. Inicialmente, a mola está comprimida de 2,0 cm e, ao ser liberada, empurra um carrinho de massa igual a 0,20 kg. O carrinho abandona a mola quando esta atinge o seu comprimento relaxado, e percorre uma pista que termina em uma rampa. Considere que não há perda de energia mecânica por atrito no movimento do carrinho.
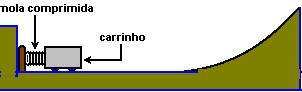
a) Qual é a velocidade do carrinho quando ele abandona a mola?
b) Na subida da rampa, a que altura o carrinho tem velocidade de 2,0 m/s?
11-(UFMG-MG) Daniel e André, seu irmão, estão parados em um tobogã, nas posições mostradas nesta figura:
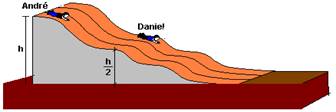
Daniel tem o dobro do peso de André e a altura em que ele está, em relação ao solo, corresponde à metade da altura em que está seu irmão. Em um certo instante, os dois começam a escorregar pelo tobogã. Despreze as forças de atrito.
É CORRETO afirmar que, nessa situação, ao atingirem o nível do solo, André e Daniel terão
a) energias cinéticas diferentes e módulos de velocidade diferentes.
b) energias cinéticas iguais e módulos de velocidade iguais.
c) energias cinéticas diferentes e módulos de velocidade iguais.
d) energias cinéticas iguais e módulos de velocidade diferentes.
12-(Ufpe-PE) Uma bolinha de massa m = 200 g é largada do repouso de uma altura h, acima de uma mola ideal, de constante elástica k = 1240 N/m, que está fixada no piso (ver figura).
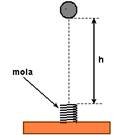
Ela colide com a mola comprimindo-a por ∆x = 10 cm. Calcule, em metros, a altura inicial h. Despreze a resistência do ar.(g=10m/s2)
13-(MACKENZIE-SP) A figura mostra o instante em que uma esfera de 4 kg é abandonada do repouso, da posição P, e cai sobre a mola ideal de constante elástica 2.102 N/m. O maior valor da velocidade atingida por essa esfera, no seu movimento descendente, é
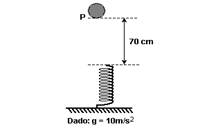
![]()
14-(Ufg) Um bloco de massa igual a 0,5 kg é abandonado, em repouso, 2 m acima de uma mola vertical de comprimento 0,8 m e constante elástica igual a 100 N/m, conforme o diagrama.
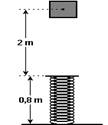
Calcule o menor comprimento que a mola atingirá. Considere g = 10 m/s2
15-(Ufpb) Um bloco de 1 kg, preso a uma mola de constante elástica 800 N/m e massa desprezível, oscila sobre um plano horizontal sem atrito com amplitude A = 0,5 m. No instante em que a energia cinética do bloco se iguala à energia potencial da mola, a velocidade do bloco vale:
![]()
16-(Ufpe-PE) Uma bolinha presa a um fio de comprimento L = 1,6 m que está fixado no teto, é liberada na posição indicada na figura (ponto A). Ao passar pela posição vertical, o fio encontra um pino horizontal fixado a uma distância h = 1,25 m (ver figura).
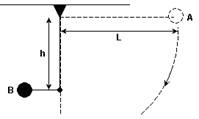
17-(UNIRIO-SP) Um carrinho de massa m=2,0kg apresentado no desenho ao lado, desliza sobre um plano horizontal com velocidade de 10m/s. No ponto A, a superfície passa a ser curva, com raio de curvatura de 2,0m.
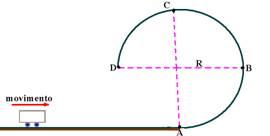
Suponha que o atrito seja desprezível ao longo de toda a trajetória e que g=10m/s2. Determine, então:
a) a aceleração centrípeta no ponto B;
b) a reação da superfície curva sobre o bloco no ponto C.
18-(UFRS-RS) Na figura, representamos uma pista em que o trecho final XYZD é um arco de circunferência. Larga-se o carrinho de massa 0,2kg no topo da pista. Despreze os atritos, considere g=10m/s2 e determine:
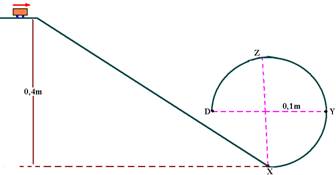
a) a energia cinética no ponto X
b) o trabalho realizado para ir de X a Y
c) a velocidade mínima com que o carrinho deve ter para passar pelo ponto Z, sem perder contato com a pista.
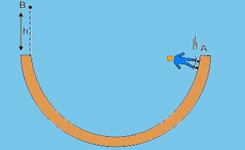
19-(UnB-DF) Em uma apresentação de circo em 1901, Allo Diavolo introduziu a acrobacia de bicicletas em pistas com loops,
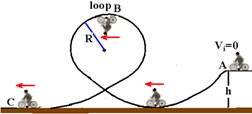
como mostra a figura. Diavolo observou que se ele partisse com velocidade zero de uma altura mínima, poderia percorrer todo o trajeto, passando inclusive pelo loop, sem cair, em um “desafio” ás leis da gravidade, conforme anunciava ele. A figurta mostra o caminho do centro de massa do sistema acrobata-bicicleta. Nessa figura, h é a altura entre o ponto mais alto – A – e o ponto mais baixo – C – da trajetória, B é o ponto mais alto do loop e Ré o raio do loop.
A partir dessas informações e considerando que m é a massa do sistema acrobata-bicicleta, que g é a aceleração da gravidade, que não há forças dissipativas, que a bicicleta não é impulsionada pelo acrobata em nenhum instante da trajetória e que apenas o movimento do centro de massa do sistema acrobata-bicicleta é analisado, julgue os itens abaixo.
1- No ponto C do caminho, mostrado na figura, a energia cinética é igual a mgh.
2- A energia mecânica total do sistema acrobata-bicicleta será mgh mesmo no caso da existência de forças dissipativas.
3- Para que o sistema acrobata-bicicleta passe pelo ponto mais alto do loop sem perder contato com a pista, o sistema deverá ter nesse ponto uma velocidade de módulo superior ou igual a ÖRg.
4- A razão entre os módulos das velocidades nos pontos B e C independe da altura h.
20- (Ufam) Uma bolinha de massa m é abandonada do ponto A de um trilho, a uma altura H do solo, e descreve a trajetória ABCD indicada na figura abaixo.
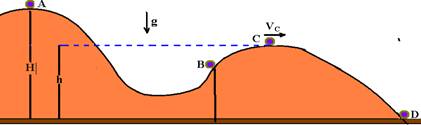
A bolinha passa pelo ponto mais elevado da trajetória parabólica BCD, a uma altura h do solo, com velocidade cujo módulo vale VC=10m/s, e atinge o solo no ponto D com velocidade de módulo igual a VD=20m/s. Podemos afirmar que as alturas referidas no texto valem: (g=10m/s2)
a) H=19m; h=14m
b) H=18m; h=10m
c) H=12m; h=4m
d) H=12m; h=15m
e) H=20m; h=15m
21-(UFJF-MG) Um trenó, com um esquimó, começa a descer por uma rampa de gelo, partindo do repouso no ponto P, à altura de 20m. Depois de passar pelo ponto Q, atinge uma barreira de proteção em R, conforme a figura.
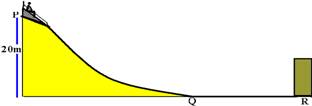
O conjunto trenó-esquimó possui uma massa total de 90kg. O trecho QR encontra-se na horizontal. Despreze as dimensões do conjunto, o atrito e a resistência do ar durante o movimento.
a) Usando o princípio da conservação da energia mecânica, calcule a velocidade com que o conjunto chega ao ponto Q na base da rampa.
b) Em R encontra-se uma barreira de proteção feita de material deformável usada para parar o conjunto após a descida. Considere que, durante o choque, a barreira não se desloca e que o conjunto se choca contra esta e pára. Sabendo que a barreira de proteção sofreu uma deformação de 1,5m durante o choque, calcule a força média exercida por ela sobre o conjunto.
22-(FUVEST-SP)
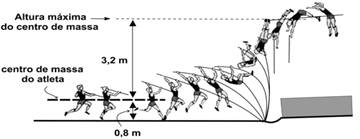
No ”salto com vara”, um atleta corre segurando uma vara e, com perícia e treino, consegue projetar seu corpo por cima de uma barra. Para uma estimativa da altura alcançada nesses saltos, é possível considerar que a vara sirva apenas para converter o movimento horizontal do atleta (corrida) em movimento vertical, sem perdas ou acréscimos de energia. Na análise de um desses saltos, foi obtida a seqüência de imagens reproduzida acima.
Nesse caso, é possível estimar que a velocidade máxima atingida pelo atleta, antes do salto, foi de, aproximadamente,
*Desconsidere os efeitos do trabalho muscular após o início do salto.
![]()
23-(UEL-PR) Uma esfera de massa m desliza, com atrito desprezível, ao longo de um trilho em laço, conforme a figura abaixo.
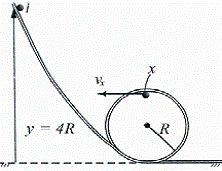
A esfera parte do repouso no ponto y = 4R acima do nível da parte mais baixa do trilho. Calcule os valore da velocidade da esfera ( vX ) e da força normal ( fN ) exercida sobre a esfera, no ponto x (ponto mais alto da trajetória circular):
24-(UFSCAR-SP) Uma formiga de massa m encontra-se no topo de uma bola de bilhar rigidamente presa ao solo.
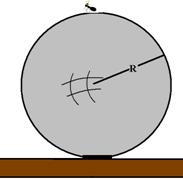
A bola possui raio R e superfície altamente polida. Considere g a aceleração da gravidade e despreze os possíveis efeitos dissipativos. A formiga começa a deslizar na bola com velocidade inicial nula.
a) Calcule o módulo da velocidade da formiga no ponto em que ela perde contato com a bola.
b) Calcule a altura do solo, em que a formiga perde contato com a bola.
25-(ITA-SP) Um pequeno bloco, solto com velocidade nula a uma altura h, move-se sob o efeito da gravidade e sem atrito sobre um trilho em forma de dois quartos de círculo de raio R, que se tangenciam, como mostra a figura.
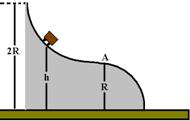
A mínima altura inicial h que acarreta a saída do bloco do trilho, após o ponto A é:
![]()
26-(UNICAMP-SP) Um carrinho de massa 300kg percorre uma montanha russa cujo trecho BCD é um arco de circunferência de raio R=5,4m, conforme a figura.
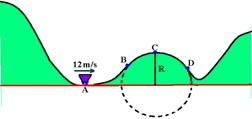
A velocidade do carrinho no ponto A é VA=12m/s. Considerando g=10m/s2 e desprezando o atrito, calcule:
a) a velocidade do carrinho no ponto C,
b) a aceleração do carrinho no ponto C,
d) a força feita pelos trilhos sobre o carrinho no ponto C.
27-(FUVEST-SP) Para testar a elasticidade de uma bola de basquete, ela é solta, a partir de uma altura Ho, em um equipamento no qual seu movimento é monitorado por um sensor. Esse equipamento registra a altura do centro de massa da bola, a cada instante,
acompanhando seus sucessivos choques com o chão. A partir da análise dos registros, é possível, então, estimar a elasticidade da bola, caracterizada pelo coeficiente de restituição CR.
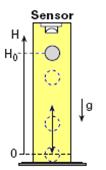
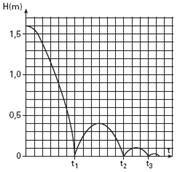
O gráfico acima apresenta os registros de alturas, em função do tempo, para uma bola de massa M = 0,60kg, quando ela é solta e inicia o movimento com seu centro de massa a uma altura Ho = 1,6m, chocando-se sucessivas vezes com o chão. A partir dessas informações:
a) Represente, no Gráfico I da folha de respostas, a energia potencial da bola, EP, em joules, em função do tempo, indicando os valores na escala.
b) Represente, no Gráfico II da folha de respostas, a energia mecânica total da bola, ET, em joules, em função do tempo, indicando os valores na escala.
c) Estime o coeficiente de restituição CR dessa bola, utilizando a definição apresentada abaixo.
NOTE E ADOTE:
– Desconsidere a deformação da bola e a resistência do ar.
– O coeficiente de restituição, CR = VR/VI, é a razão entre a velocidade com que a bola é rebatida pelo chão (VR) e a velocidade com que atinge o chão (VI), em cada choque. Esse coeficiente é aproximadamente constante nas várias colisões.
28-(UFSCAR-SP) Idéia para a campanha de redução de acidentes: enquanto um narrador exporia fatores de riscos nas estradas, uma câmera mostraria o trajeto de um sabonete que, a partir do repouso de um ponto sobre a borda de uma banheira, escorregaria para o interior da mesma, sofrendo um forte impacto contra a parede vertical oposta.

Para a realização da filmagem, a equipe técnica, conhecendo a aceleração da gravidade (10m/s2) e desconsiderando qualquer atuação de forças contrárias ao movimento, estimou que a velocidade do sabonete, momentos antes de seu impacto contra a parede da banheira, deveria ser um valor, em m/s, mais próximo de:
![]()
29-(CESGRANRIO-RJ) Uma esfera de massa 0,10kg rola sobre o perfil da montanha russa mostrado na figura abaixo.
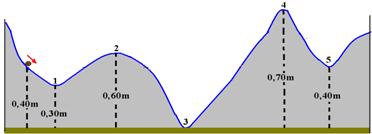
No instante representado, ela se move para baixo (veja seta) com energia cinética igual a 0,10J. Embora o atrito seja muito pequeno, a bola acabará parando na posição: (g=10m/s2)
![]()
30-(Ufla-MG) Um parque aquático tem um toboágua, conforme a figura.
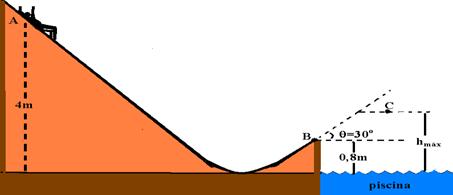
Um indivíduo de 60kg desliza pelo toboágua a partir do ponto A, sendo lançado numa piscina de uma altura de 0,8m, ponto B, numa direção que faz um ângulo de 30o com a horizontal.
Considerando o atrito desprezível, g=10m/s2 e cós30o=Ö3/2, calcule:
a) a velocidade do indivíduo ao deixar o toboágua no ponto B
b) a energia cinética do indivíduo no ponto mais alto da trajetória, ponto C.
c) a altura do ponto C, hmáx.
31- (ITA-SP) Um aro de1 kg de massa encontra-se preso a uma mola de massa desprezível, constante elástica k = 10 N/m e comprimento inicial L = 1 m quando não distendida, afixada no ponto O. A figura mostra o aro numa posição P em uma barra horizontal fixa ao longo da qual o aro pode deslizar sem atrito.
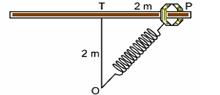
Soltando o aro do ponto P, qual deve ser sua velocidade, em m/s, ao alcançar o ponto T, a 2 m de distância?
32- (UNESP-SP) No esporte conhecido como “ioiô humano”, o praticante, preso à extremidade de uma corda elástica, cai da beira de uma plataforma para as águas de um rio. Sua queda é interrompida, a poucos metros da superfície da água, pela ação da corda elástica, que tem a outra extremidade firmemente presa à beira da plataforma.
Suponha que, nas condições citadas acima, a distensão máxima sofrida pela corda, quando usado por um atleta de peso 750 N, é de 10 metros, e que seu comprimento, quando não distendida, é de 30 metros. Nestas condições:
a) A que distância da plataforma está o atleta, quando chega ao ponto mais próximo da água?
b) Qual o valor da constante elástica da corda?
(Despreze o atrito com o ar e a massa da corda, e considere igual a zero o valor da velocidade do atleta no início da queda.)
Sistemas dissipativos
33-(UFSCAR-SP) O trabalho realizado por uma força conservativa independe da trajetória, o que não acontece com as forças dissipativas, cujo trabalho realizado depende da trajetória. São bons exemplos de forças conservativas e dissipativas, respectivamente,
a) peso e massa.
b) peso e resistência do ar.
c) força de contato e força normal.
d) força elástica e força centrípeta.
e) força centrípeta e força centrífuga.
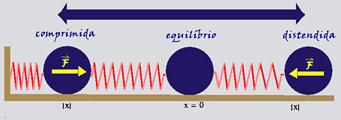
34-(UNIFESP-SP) Na figura estão representadas duas situações físicas cujo objetivo é ilustrar o conceito de trabalho de forças conservativas e dissipativas.

Em I, o bloco é arrastado pela força ù sobre o plano horizontal; por causa do atrito, quando a força ![]() cessa o bloco pára. Em II, o bloco, preso à mola e em repouso no ponto O, é puxado pela força
cessa o bloco pára. Em II, o bloco, preso à mola e em repouso no ponto O, é puxado pela força ![]() sobre o plano horizontal, sem que sobre ele atue nenhuma força de resistência; depois de um pequeno deslocamento, a força cessa e o bloco volta, puxado pela mola, e passa a oscilar em torno do ponto O.
sobre o plano horizontal, sem que sobre ele atue nenhuma força de resistência; depois de um pequeno deslocamento, a força cessa e o bloco volta, puxado pela mola, e passa a oscilar em torno do ponto O.
Essas figuras ilustram:
a) I: exemplo de trabalho de força dissipativa (força de atrito), para o qual a energia mecânica não se conserva;
II: exemplo de trabalho de força conservativa (força elástica), para o qual a energia mecânica se conserva.
b) I: exemplo de trabalho de força dissipativa (força de atrito), para o qual a energia mecânica se conserva;
II: exemplo de trabalho de força conservativa (força elástica), para o qual a energia mecânica não se conserva.
c) I: exemplo de trabalho de força conservativa (força de atrito), para o qual a energia mecânica não se conserva;
II: exemplo de trabalho de força dissipativa (força elástica), para o qual a energia mecânica se conserva.
d) I: exemplo de trabalho de força conservativa (força de atrito), para o qual a energia mecânica se conserva;
II: exemplo de trabalho de força dissipativa (força elástica), para o qual a energia mecânica não se conserva.
e) I: exemplo de trabalho de força dissipativa (força de atrito);
II: exemplo de trabalho de força conservativa (força elástica), mas em ambos a energia mecânica se conserva.
35-(FGV-SP) Devido a forças dissipativas, parte da energia mecânica (E) de um sistema foi convertida em calor, circunstância caracterizada pelo gráfico apresentado

Sabendo-se que a variação da energia potencial desse sistema foi nula, o trabalho realizado sobre o sistema nos primeiros 4 segundos, em J, foi, em módulo,
![]()
36-(FGV-SP) Ao passar pelo ponto A, a uma altura de 3,5m do nível de referência B, uma esfera de massa 2kg, que havia sido abandonada de um ponto mais alto que A, possui velocidade de 2m/s. A esfera passa por B e, em C, a 3,0m do mesmo nível de referência, sua velocidade torna-se zero.
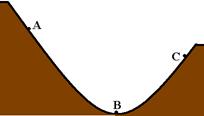
A parcela de energia dissipada por ações resistentes sobre a esfera é, em J.
Dados: g=10m/s2
![]()
37-(Uece) Na presença da atmosfera terrestre, um projétil, lançado verticalmente para cima, perde parte de sua energia devido a forças viscosas com o ar. Tal perda pode ser minimizada tornando o projétil mais aerodinâmico. Caso fosse possível eliminar uma perda de 40 kJ neste processo, devido a essas melhorias aerodinâmicas, de quanto aumentaria, aproximadamente, a altura máxima atingida por um projétil de 10 kg lançado verticalmente para cima?
Admita que a aceleração da gravidade não varie e que seja igual a 10 m/s2.
![]()
38-(UFMG-MG) Observe o perfil de uma montanha russa representado nesta figura:
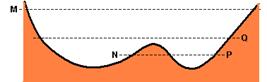
Um carrinho é solto do ponto M, passa pelos pontos N e P e só consegue chegar até o ponto Q. Suponha que a superfície dos trilhos apresenta as mesmas características em toda a sua extensão. Sejam E(cn) e E(cp) as energias cinéticas do carrinho, respectivamente, nos pontos N e P e E(tp) e E(tq) as energias mecânicas totais do carrinho, também respectivamente, nos pontos P e Q. Considerando-se essas informações, é CORRETO afirmar que
a) E(cn) = E(cp) e E(tp) = E(tq).
b) E(cn) = E(cp) e E(tp) > E(tq).
c) E(cn) > E(cp) e E(tp) = E(tq).
d) E(cn) > E(cp) e E(tp) > E(tq).
39-(UEA-AM) Na situação descrita a seguir, uma esfera de massa 4,0kg é abandonada do repouso da altura de 8,0m.
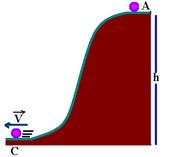
Ela percorre a rampa passando pelo ponto horizontal com velocidade de 10m/s. (g=10m/s2) Qual a porcentagem da energia dissipada por atrito entre os pontos A e C?
![]()
40-(PUC-SP) O carrinho da figura tem massa 100g e encontra-se encostado em uma mola de constante elástica 100N/m, comprimida de 10cm.
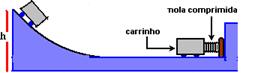
Ao ser liberado, o carrinho sobe a rampa até uma altura máxima de 30cm. O módulo da quantidade de energia mecânica dissipada no processo, em joules, é:
![]()
41-(UNESP-SP) Um carrinho de 2,0kg, que dispõe de um gancho, movimenta-se sobre um plano horizontal, com velocidade de 1,0m/s, em direção à argola presa na extremidade do fio mostrado na figura. A outra extremidade do fio está presa a um bloco, de peso 5,0N, que se encontra em repouso sobre uma prateleira.
Enganchando-se na argola, o carrinho puxa o fio e eleva o bloco, parando momentaneamente quando o bloco atinge a altura máxima h acima da prateleira.
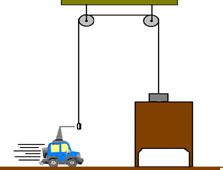
Nessas condições, determine: (g=10m/s2).
a) a energia cinética inicial do carrinho
b) a altura h, supondo que ocorra perda de 20% da energia cinética inicial do carrinho quando o gancho se prende na argola.
Observações: Despreze quaisquer atritos e as massas das polias.
42-(PUC-SP) Uma criança de massa 25 kg, inicialmente no ponto A, distante 2,4 m do solo, percorre, a partir do repouso, o escorregador esquematizado na figura. O escorregador pode ser considerado um plano inclinado cujo ângulo com a horizontal é de 37°. Supondo o coeficiente de atrito cinético entre a roupa da criança e o escorregador igual a 0,5, a velocidade com que a criança chega à base do escorregador (ponto B) é, em m/s, (g=10m/s2)
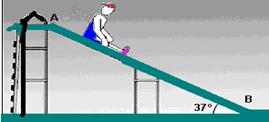
Dados: sen 37° = 0,6; cos 37° = 0,8; tg 37° = 0,75
![]()
43-(FUVEST-SP) Uma pista é formada por duas rampas inclinadas, A e B, e por uma região horizontal de comprimento L. Soltando-se, na rampa A, de uma altura HÁ, um bloco de massa m, verifica-se que ele atinge uma altura HB (figura), em experimento realizado na Terra.

O coeficiente de atrito cinético entre o bloco e a pista é nulo nas rampas e igual a m na região horizontal. Suponha que esse mesmo experimento seja realizado em Marte, onde a aceleração da gravidade é gM=g/3, e considere que o bloco seja solto na mesma rampa A e da mesma altura HA. Determine:
a) a razão Ra=VxTerra/VxMarte entre as velocidades do bloco no final da rampa A (ponto x), em cada uma das experiências (Terra e Marte)
b) a razão Rb=WTerra/WMarte, entre as energias mecânicas dissipadas pela força de atrito na região horizontal, em cada uma das experiências (Terra e Marte).
44-(ITA-SP) A partir do repouso, um carrinho de montanha russa desliza de uma altura H=20Ö3m sobre uma rampa de 60o de inclinação e corre 2om num trecho horizontal antes de chegar em um loop circular, de pista sem atrito.
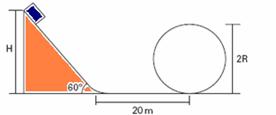
Sabendo que o coeficiente de atrito da rampa e do plano horizontal é 0,5, assinale o valor do raio máximo que pode ter esse loop para que o carrinho faça todo o percurso sem perder contato com a pista.
a) R=8√3m
b) R=4(√3 – 1)m
c) R=8(√3 – 1)m
d) R=4(2√3 – 1)m
e) R=40(√3 – 1)/3m
45-(UF-RR) Uma bola de borracha, de massa igual a 1,0kg, cai de uma altura de 2,0m, em relação ao solo, com velocidade inicial nula. Ao tocar o solo, a bola transfere para este 12J, na forma de calor e, e volta a subir verticalmente.
Considere a aceleração da gravidade g=10m/s2. A altura, em cm, atingida pela bola na subida é de:
![]()
46-(UFOP-MG) Um jogador de basquete treina com uma bola cuja massa é de 2 kg. A bola é

abandonada a 1 m de altura e,ao chocar-se com o solo, perde 50 % de sua energia. Usando g= 10 m/s2, calcule:
a) a energia cinética da bola imediatamente após o primeiro choque;
b) a velocidade da bola ao atingir o solo pela segunda vez;
c) depois de qual choque a bola irá adquirir a energia aproximada de 0,08 J.
47-(UFF-RJ) Dois brinquedos idênticos, que lançam dardos usando molas, são disparados
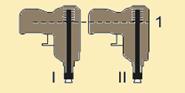
simultaneamente na vertical para baixo. As molas com os respectivos dardos foram inicialmente comprimidas até a posição 1 e, então, liberadas. A única diferença entre os dardos I e II, conforme mostra a figura, é que I tem um pedaço de chumbo grudado nele, o que não existe em II.
Escolha o gráfico que representa as velocidades dos dardos I e II, como função do tempo, a partir do instante em que eles saem dos canos dos brinquedos.

(UFU-MG) TEXTO PARA AS PRÓXIMAS 3 QUESTÕES:
O tiro com arco é um esporte olímpico desde a realização da segunda olimpíada em Paris, no ano de 1900. O arco é um dispositivo que converte energia potencial elástica, armazenada quando a corda do arco é tensionada, em energia cinética, que é
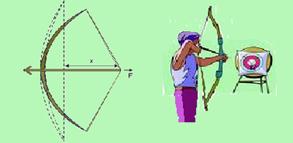
transferida para a flecha.Num experimento, medimos a força F necessária para tensionar o arco até uma certa distância x, obtendo os seguintes valores:

48-(UFU-MG) O valor e unidades da constante elástica, k, do arco são:
![]()
49-(UFU-MG) Ao tensionar o arco, armazena-se energia potencial elástica no sistema. Sendo assim, a expressão para a energia potencial armazenada é:
![]()
50-(UFU-MG) Se a massa da flecha é de 10 gramas, a altura h=1,40 m e a distância x=1m, a velocidade com que ela é disparada é:
![]()
51-(UERJ-RJ) Os esquemas a seguir mostram quatro rampas AB, de mesma altura AC e perfis distintos, fixadas em mesas idênticas, nas quais uma pequena pedra é abandonada, do ponto A, a partir do repouso.

Após deslizar sem atrito pelas rampas I, II, III e IV, a pedra toca o solo, pela primeira vez, a uma distância do ponto B respectivamente igual a dI, dII, dIII e dIV.A relação entre essas distâncias está indicada na seguinte alternativa:
a) dI > dII = dIII > dIV
b) dIII > dII > dIV > dI
c) dII > dIV = dI > dIII
d) dI = dII = dIII = dIV
52-(FATEC-SP) Um skatista brinca numa rampa de skate conhecida por “half pipe”. Essa pista tem como corte transversal uma semicircunferência de raio 3 metros, conforme mostra a figura. O atleta, saindo do extremo A da pista com velocidade de 4
m/s, atinge um ponto B de altura máxima h. Desconsiderando a ação de forças dissipativas e adotando a aceleração da gravidade g = 10 m/s2, o valor de h, em metros, é de
![]()
53-(UNESP-SP) O Skycoaster é uma atração existente em grandes parques de diversão, representado nas figuras a seguir. Considere que em um desses brinquedos, três aventureiros são presos a cabos de aço e içados a grande altura. Os jovens, que se

movem juntos no brinquedo, têm massas iguais a 50 kg cada um. Depois de solto um dos cabos, passam a oscilar tal como um pêndulo simples, atingindo uma altura máxima de 60 metros e chegando a uma altura mínima do chão de apenas 2 metros. Nessas condições e desprezando a ação de forças de resistências, qual é, aproximadamente, a máxima velocidade, em m/s, dos participantes durante essa oscilação e qual o valor da maior energia cinética, em kJ, a que eles ficam submetidos?
54-(UECE-CE) A figura a seguir mostra quatro trajetórias de uma bola de futebol lançada no espaço.
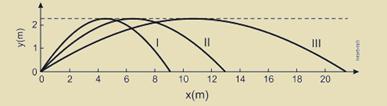
Desconsiderando o atrito viscoso com o ar, assinale o correto.
a) A trajetória que exigiu a maior energia foi a I.
b) A trajetória que exigiu a maior energia foi a II.
c) A trajetória que exigiu a maior energia foi a III.
d) A energia exigida é a mesma para todas as trajetórias.
55-(UECE-CE) Um carrinho de montanha russa tem velocidade igual a zero na posição 1, indicada na
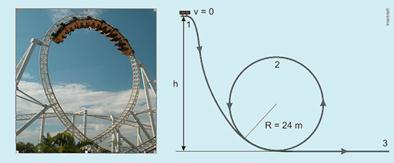
figura a seguir, e desliza no trilho sem atrito, completando o círculo até a posição 3. A menor altura h, em metros, para o carro iniciar o movimento sem que venha a sair do trilho na posição 2 é
![]()
56-(FGV-RJ) O gráfico abaixo representa a energia potencial EP, em função do tempo, de uma
pequena esfera em movimento oscilatório, presa na extremidade de uma mola. Dentre os gráficos I, II, III e IV, aqueles que representam a energia cinética e a energia total do sistema, quando não há efeitos dissipativos, são, respectivamente,

a) I e II.
b) I e III.
c) II e III.
d) II e IV.
e) III e I.
57-(FUVEST-SP) Um esqueitista treina em uma pista cujo perfil está representado na figura abaixo. O trecho horizontal AB está a uma altura h = 2,4 m em relação ao trecho, também horizontal, CD. O esqueitista percorre a pista no sentido de A para D.
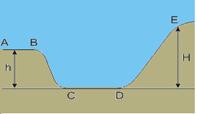
No trecho AB, ele está com velocidade constante, de módulo v = 4 m/s; em seguida, desce a rampa BC, percorre o trecho CD, o mais baixo da pista, e sobe a outra rampa até atingir uma altura máxima H, em relação a CD. A velocidade do esqueitista no trecho CD e a altura máxima H são, respectivamente, iguais a

a) 5 m/s e 2,4 m.
b) 7 m/s e 2,4 m.
c) 7 m/s e 3,2 m.
d) 8 m/s e 2,4 m.
e) 8 m/s e 3,2 m.
58-(UNIFESP-SP) Um dos brinquedos prediletos de crianças no verão é o toboágua. A emoção do brinquedo está associada à grande velocidade atingida durante a descida, uma vez que o atrito pode ser desprezado devido à presença da água em todo o percurso do brinquedo, bem como à existência das curvas fechadas na horizontal, de forma que a criança percorra esses trechos

encostada na parede lateral (vertical) do toboágua. Sabendo que a criança de 36 kg parte do repouso, de uma altura de 6,0 m acima da base do toboágua, colocado à beira de uma piscina, calcule: Dado: g = 10,0 m/s2
a) A força normal, na horizontal, exercida sobre a criança pela parede lateral do toboágua, no ponto indicado na figura (curva do toboágua situada a 2,0 m da sua base) onde o raio de curvatura é igual a 80 cm.
b) A força dissipativa média exercida pela água da piscina, necessária para fazer a criança parar ao atingir 1,5 m de profundidade, considerando que a criança entra na água da piscina com velocidade, na vertical, aproximadamente igual a 10,9 m/s, desprezando-se, neste cálculo, a perda de energia mecânica no impacto da criança com a água da piscina.
59-(UFG-GO) Uma mola ideal é usada para fornecer energia a um bloco de massa m, inicialmente em repouso, o qual mover-se sem atrito em toda a superfície, exceto entre os pontos A e B. Ao liberar o sistema massa-mola, o bloco passa pelo ponto P com energia cinética de 1/20 da energia potencial gravitacional.
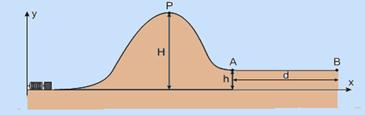
Considerando o exposto, com h = 0,15H e d = 3H, calcule:
a) o valor numérico do coeficiente de atrito para que o bloco pare no ponto B;
b) a porcentagem da energia total dissipada pela força de atrito.
60-(UFLA-MG) Um esquilo “voador” consegue planar do alto de uma árvore, a uma altura de 10 m até o chão, com

velocidade constante de 5 m/s. Considerando a aceleração da gravidade g = 10 m/s2 e a massa do esquilo 2 kg, é CORRETO afirmar que o trabalho da força de sustentação que atua sobre o esquilo ao longo desse deslocamento é de
![]()
61-(FUVEST-SP) Usando um sistema formado por uma corda e uma roldana, um homem levanta uma caixa de massa m, aplicando na corda uma força F que forma um ângulo θ com a direção vertical, como mostra a figura. O trabalho realizado pela resultante das forças que atuam na caixa – peso e força da corda -, quando o centro de massa da caixa é elevado, com velocidade constante v, desde a altura ya até a altura yb, é:
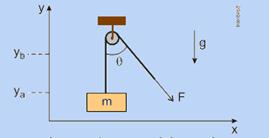
a) nulo.
b) F (yb – ya).
c) mg (yb – ya).
d) F cos θ (yb – ya).
e) mg (yb – ya) + mv2/2.
62-(UFSM-RS) Não se percebe a existência do ar num dia sem vento; contudo, isso não significa que ele não existe.

Um corpo com massa de 2kg é abandonado de uma altura de 10m, caindo verticalmente num referencial fixo no solo. Por
efeito da resistência do ar, 4J da energia mecânica do sistema corpo-Terra se transformam em energia interna do ar e do
corpo. Considerando o módulo de aceleração da gravidade como g= 10m/s2, o corpo atinge o solo com velocidade de módulo,
em m/s, de
![]()
63-(UFJF-MG) A figura ao lado mostra um sistema composto por dois blocos de massas idênticas m m kg A B = = 3,0 e uma mola de constante elástica k N m = 4,0 / . O bloco A está preso a um fio de
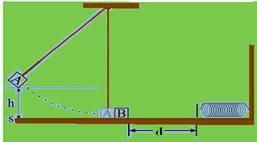
massa desprezível e suspenso de uma altura h m = 0,8 em relação à superfície S , onde está posicionado o bloco B . Sabendo que a distância entre o bloco B e a mola é d m = 3,0 e que a colisão entre os blocos A e B é elástica, faça o que se pede nos itens seguintes
a) Usando a lei de conservação da quantidade de movimento (momento linear), calcule a velocidade do bloco B imediatamente após a colisão do bloco A .
b) Calcule o deslocamento máximo sofrido pela mola se o atrito entre o bloco B e o solo for desprezível.
c) Calcule a distância deslocada pelo bloco B em direção à mola, se o atrito cinético entre o bloco B e o solo for igual a μ=0,4. Nesse caso, a mola será comprimida pelo bloco B ? Justifique.
64-(UFBA-BA) Uma esfera rígida de massa m1 = 0,5kg, presa por um fio de comprimento L = 45,0cm e massa desprezível, é suspensa em uma posição tal que, como mostra a figura, o fio suporte faz um ângulo de 90o com a direção vertical.
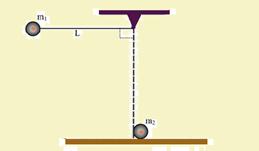
Em um dado momento, a esfera é solta, indo se chocar com outra esfera de massa m2 = 0,5kg, posicionada em repouso no solo.
Considerando o diâmetro das esferas desprezível e o choque entre elas perfeitamente elástico, determine a velocidade das esferas após o choque, supondo todas as forças dissipativas desprezíveis, o módulo da aceleração da gravidade local igual a 10m/s2 e o
coeficiente de restituição ε=(V2’ – V1’)/(V1 – V2) em que V1’ e V2’ são as velocidades finais das esferas e v1 e v2 as velocidades iniciais.
65-(UFF-RJ)

Dois objetos feitos do mesmo material repousam sobre um trecho sem atrito de uma superfície horizontal, enquanto comprimem uma mola de massa desprezível.
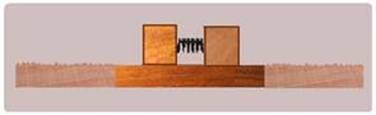
Quando abandonados, um deles, de massa 2,0 kg, alcança a velocidade de 1,0 m/s ao perder o contato com a mola. Em seguida, alcança um trecho rugoso da superfície, passa a sofrer o efeito do atrito cinético e percorre 0,5 m nesse trecho até parar.
a) Qual o coeficiente de atrito cinético entre esse bloco e o trecho rugoso da superfície horizontal?
b) Qual é a velocidade alcançada pelo 2º bloco, de massa 1,0 kg, ao perder o contato com a mola?
c) Sabendo-se que a constante elástica da mola é 6,0.104 N/m, de quanto a mola estava comprimida inicialmente?
66-(FGV-SP)

Em algumas estações de trem, há rígidas molas no fim dos trilhos com a finalidade de amortecer eventual colisão de um trem, cujo maquinista não consiga pará-lo corretamente junto à plataforma. Certa composição, de massa total 2 m, parada bem próxima à mola de constante k, relaxada, recebe um impacto de outra composição, de massa m, vindo a uma velocidade v, que acaba engatando na primeira. Ambas vão comprimir a mola, causando-lhe uma deformação máxima x ao pararem instantaneamente, como mostram os esquemas.
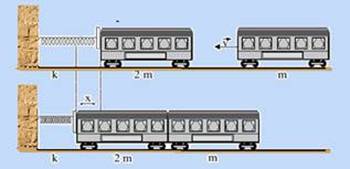
Desprezando a ação de agentes externos e dissipativos, a expressão de x, em função de k, m e v, será
(A) x = (m · v) ∕ (3 · k).
(B) x = (m · v2) ∕ (3 · k).
(C) x = (v / 3) · √(m/ k)
(D) x = v · √(3·m) / k .
(E) x = v ·√ m/ (3k).
67-(UEPG-PR)

Um corpo está suspenso por um fio inextensível. Conforme é mostrado abaixo, o corpo é afastado
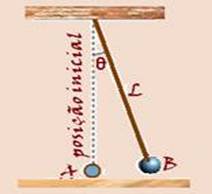
da sua posição inicial A e deslocado até B, onde é solto e começa a oscilar. Com relação à energia mecânica do sistema e desprezando as forças externas que poderão atuar sobre ele, assinale a alternativa correta.
a) Quando o corpo passa pela posição A, a energia mecânica do sistema é nula.
b) A energia total do sistema independe do afastamento do corpo da posição inicial.
c) Em qualquer ponto do sistema o somatório das energias potencial e cinética é igual à energia mecânica do sistema.
d) A energia mecânica total do sistema depende do comprimento do fio (L).
e) Em B, a energia cinética do sistema é máxima e a potencial nula.
68-(PUC-RJ)

Um ciclista tentando bater um recorde de velocidade em uma bicicleta desce, a partir do repouso, a distância de 1440 m em uma
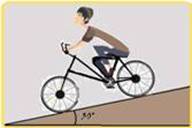
montanha cuja inclinação é de 30°.
Calcule a velocidade atingida pelo ciclista ao chegar à base da montanha.
Dados: Não há atrito e g = 10 m/s2
(A) 84 m/s
(B) 120 m/s
(C) 144 m/s
(D) 157 m/s
(E) 169 m/s
69–COLÉGIO NAVAL)

Analise a figura a seguir.

Dados: g=10m/s2 e Mtrenó=800kg.
Numa determinada montanha russa um trenó, sob a ação de uma força resultante constante, que atua de A até B, parte do repouso do ponto A e, após 2 segundos, atinge a velocidade de 180 km/h no ponto B, iniciando uma subida que o leva até o ponto C, onde passa com velocidade de 18 km/h. Sabendo que a energia perdida pelos atritos entre os pontos B e C foi de 19.104J, é correto afirmar que a força resultante ![]() que atuou sobre o trenó entre os pontos A e B e a altura atingida por ele no ponto C são, respectivamente:
que atuou sobre o trenó entre os pontos A e B e a altura atingida por ele no ponto C são, respectivamente:
(A) 10000 N e h = 80m
(B) 20000 N e h = 80m
(C) 20000 N e h = 100m
(D) 40000 N e h = 100m
(E) 80000 N e h = 120m
70-(EsPCEx)

Um corpo de massa 4 kg está em queda livre no campo gravitacional da Terra e não há nenhuma força dissipativa

atuando. Em determinado ponto, ele possui uma energia potencial, em relação ao solo, de 9 J, e sua energia cinética vale 9 J. A velocidade do corpo, ao atingir o solo, é de:
[A] 5 m/s
[B] 4 m/s
[C] 3 m/s
[D] 2 m/s
[E] 1 m/s
71-(ENEM-MEC)

Uma das modalidades presentes nas olimpíadas é o salto com vara. As etapas de um dos saltos de um atleta estão representadas na figura:

Desprezando-se as forças dissipativas (resistência do ar e atrito), para que o salto atinja a maior altura possível, ou seja, o máximo de energia seja conservada, é necessário que
A. a energia cinética, representada na etapa I, seja totalmente convertida em energia potencial elástica, representada na etapa IV.
B. a energia cinética, representada na etapa II, seja totalmente convertida em energia potencial gravitacional,
representada na etapa IV.
C. a energia cinética, representada na etapa I, seja totalmente convertida em energia potencial elástica representada na etapa III.
D. a energia potencial gravitacional, representada na etapa II, seja totalmente convertida em energia potencial elástica, representada na etapa IV.
E. a energia potencial gravitacional, representada na etapa I, seja totalmente convertida em energia potencial elástica, representada na etapa III.

